射影几何中有一个重要的定理，那就是帕斯卡定理。它的定义是，如果一个六边形内接在一个二次曲线上，那么它的三条对边的交点在同一条直线上，这个验证可以通过几何画板来完成。那么几何画板如何验证帕斯卡定理？接下来，边肖会给你答案。

验证步骤:

画一个内接六边形ABCDEF的圆

打开课件制作工具，随意选择圆工具画一个圆，然后用点工具在圆上画A、B、C、D、E、F点，再用线段工具依次连接两个相连的点，从而画出圆的内切六边形。

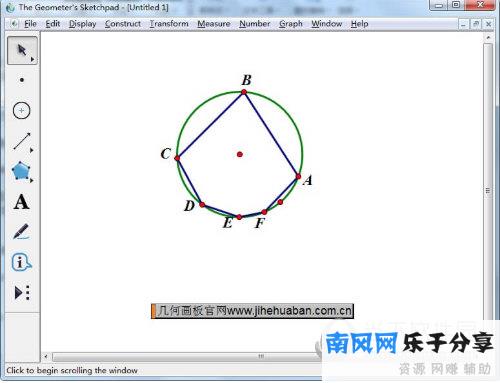
步骤2验证三对相对边的交点在同一条直线上

1.延伸边AB和de在点g相交。

选择光线工具，使光线BA和DE。两条射线相交，交点标记为点g，如下图所示。

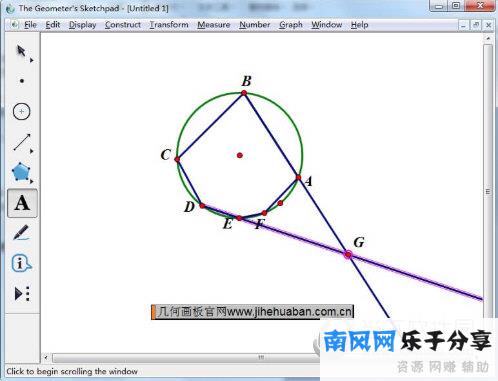
2.延伸边BC和EF在点h相交。

选择光线工具，制作光线BC和EF。两条射线相交，交点标记为H点，如下图所示。

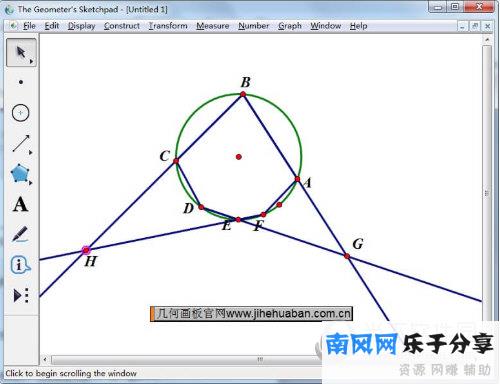
3.延伸侧CD和FA在点K相遇。

选择光线工具，制作光线CD和FA。两条射线相交，交点标记为点k，如下图所示。

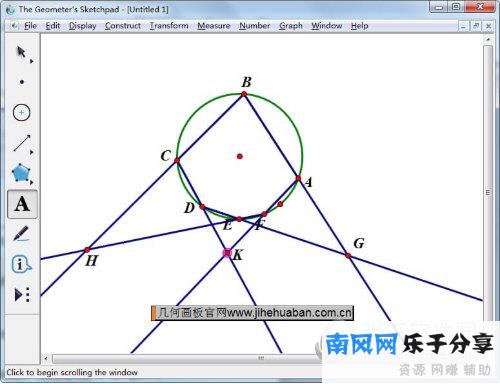
4.连接G、H和K，并确认三个交点共线

选择一个直线工具，做一条直线HG，发现G、H、K三点在同一条直线上，从而验证了帕斯卡定理。

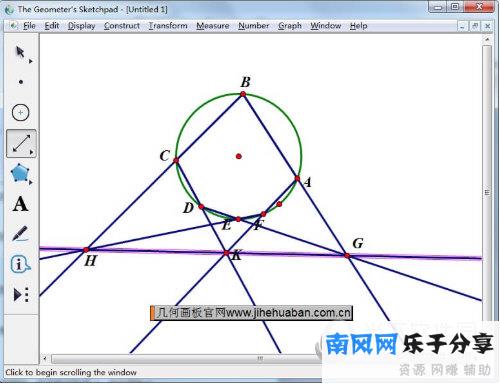
以上是《几何画板》上帕斯卡定理的验证方法。希望本教程对几何画板软件的用户有所帮助。相信大家看了以上步骤，大致掌握了具体方法，自己去验证一下吧。